A Bloom filter is a data structure that keeps track of objects without actually storing them.
In this post, I will discuss the exact workings of a bloom filter, including its use in practice. After that, I will show you how to implement a simple but high-performance bloom filter in C++. I will also show some performance measurements, showing the relation between the complexity of the filter (in number of hash calculations done) and the false-positive rate during testing.
How does it work?
A Bloom filter is a way to keep track of objects without actually storing the objects themselves. This obviously means that the Bloom filter cannot be used to retrieve any objects, it simply tracks whether it has seen an object before or not.
Knowing whether an object has been seen before can be useful for things like web caching, malware detection etc. The advantage of using a Bloom filter over a (hash based) set/dictionary is that the lookup can be done much faster, as there is no need to traverse large amounts of memory or disk space during the lookup.
Implementation
Bloom filters support two actions, keeping track of an object and checking whether an object has been seen before.
Adding objects to the Bloom filter:
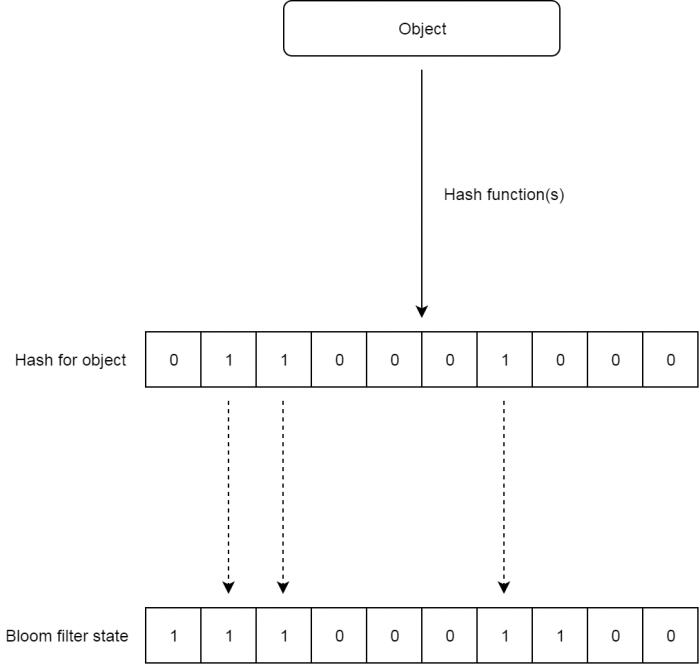
- Calculate hash values for the object to add;
- Use these hash-values to set certain bits in the Bloom filter state (hash value is the index of the bit to set).
Checking whether the Bloom filter contains an object:
- Calculate hash values for the object to add;
- Check whether the bits indexed by these hash values are set in the Bloom filter state.
The earlier shown figure illustrates how adding and checking works. Keep in mind that the hash value for an object is not directly added to the bloom filter state, each hash function simply determines which bit to set or to check. For example: if only one hash function is used, only one bit is set or checked.
A C++ implementation of this algorithm can be found here: C++ Bloom filter.
Measurements/setup
The exact algorithm is displayed on the Github page linked earlier, but I will quickly show the most important features of this algorithm.
| Hashing algorithm used | MD5 |
| Total memory needed | 8 KB |
To determine the rate of false-positives of the Bloom filter, a dataset of the top 5000 most viewed Wikipedia pages has been used. We simply initialize the Bloom filter with 500 randomly-picked page titles from this document and test whether the Bloom filter correctly identifies the other 4500 titles as never seen before.
With a little bit of math (which I will not go into in this post), we can calculate the expected rate of false positives based on the formula:
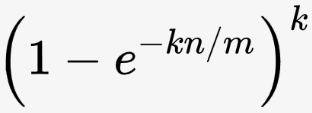
In this formula, k denotes the number of hash functions (i.e. the number of indices of bits to set), n is the total amount of objects stored in the Bloom filter (which is 10% of the total training set of 5000 objects) and m denotes the size of the Bloom filter state in bits (which is 8 KB = 65536 bits).
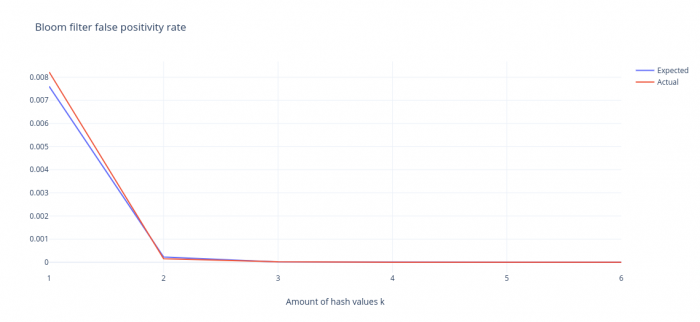
The table below shows the amount of hash values to use (parameter k), the expected false positivity rate (according to the displayed formula) and the actual false positivity rate.
| k | 1 | 2 | 3 | 4 | 5 | 6 |
| Expected false positivity rate | 0.00760 | 0.000229 | 1.16e-5 | 8.16e-7 | 7.35e-8 | 8.02e-9 |
| Actual false positivity rate | 0.00822 | 0.000155 | 2.22e-5 | 0 | 0 | 0 |
It is important to use a good hash function, one that has uniformity in output values, that is: all hash results have the same likelihood of appearing for a random object. Using a hash function like std::hash (the C++ built-in hash method) will result in a much higher rate of false-positives as more output values collide (meaning they are the same for different actual objects).
Since calculating MD5 hashes is (relatively) slow, only one MD5 hash value is calculated, which is then split up into k different values. This means only one MD5 hashing operation has to be done instead of actually doing k hashing operations.
Conclusion
Using a Bloom filter is a really fast and space-efficient way of keeping track of objects when there is no need to actually store these objects. By using a large enough storage state and the right amount of hash values, the number of false positives can be kept low in practice.
The source code, the dataset and the results are available at: https://github.com/daankolthof/bloomfilter.