When we use graph-based data in our programs, we need to decide on the best way to structure, represent and store information on these graphs. Furthermore, we need to use certain algorithms to process the data within these graphs.
C++, and practically every other programming language, provides ways of implementing all of this ourselves. However, for the sake of simplicity, development speed and code correctness, it is usually preferred to use an existing library that provides the functionality you need.
In this post, I am analysing the Boost Graph Library, showing its strengths and weaknesses. I am also showing the built-in support for some of the most common graph algorithms.
The Boost Graph Library
The Boost Graph Library is a C++ library that provides the following graph-related functionality:
- Representation of graph data in multiple formats.
- Algorithms for graph traversal, ordering, analysis, etc.
Graph Types
There are three different graph types within the library. These graph types are characterised by the way they store data on vertices and edges. In this section, we’ll analyse the different data structures for the two most important graph types as well as their advantages and disadvantages.
Adjacency list
The adjacency list consists of a list of vertices in the graph and, for each vertex, a list of edges to other vertices.

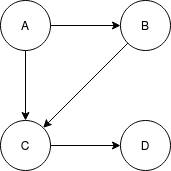
As shown above, an adjacency list consists of two separate elements: a vertex list and an edge list. These lists can be implemented using several different data structures. The choice of these data structures will have an impact on the runtime and functionality of the graph.
Vertex List
A list of all vertices present in the graph, this vertex list will also contain a reference to the edge list for each vertex in the graph. The vertex list has to be implemented either using a sequence-based container such as an std::list or a random-access-based container such as an std::vector.
The difference between these is that removing a vertex is done in constant time on a sequence-based vertex list, while a random-access-based vertex list requires linear time: O(V + E) with V being the number of vertices and E being the number of edges. This happens because the edge list stores references to indices of the vertex vector, which will have to be updated after removing an element from said vector.
In terms of memory requirements, an std::vector requires less memory per element and stores the elements in continuous memory, which in practice means improved iteration performance due to cache locality.
Edge List
A list of all outgoing edges for a vertex. When the graph itself is bidirectional (as opposed to single-directional or undirected), each vertex will also a have list of incoming edges. The edge list has to be implemented using either a sequence-based container such as std::list or std::vector or a unique associative container such as std::set.
Using a unique associative container will ensure that the graph, after construction, does not contain parallel edges. This happens because edges are stored based on their target/destination and unique associative containers can only store one element per key (target/destination).
Adjacency Matrix
An adjacency matrix is a V*V matrix where each element in the matrix denotes an edge.
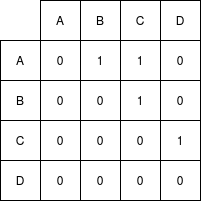

The data structure powering this graph type is a simple 2-dimensional array. The adjacency matrix works well when a graph is relatively dense, as the memory usage is only dependent on the number of vertices, not the number of edges.
Due to the way the edges are stored, checking for an edge between two vertices, as well as adding or removing said edges, is done in constant time. The main disadvantage of the adjacency matrix is that retrieving all edges is done in O(V*V) instead of O(V + E), as we will need to check each (source, target) vertex pair to check for an edge between them. This can be a disadvantage in algorithms that traverse the entire graph (depth-first search, breadth-first search, Dijkstra’s, etc.).
Measurements
As iterating over edges within a graph is a common use-case for many graph algorithms, I have done some measurements for the Adjacency Matrix graph type, showing the quadratic increase in runtime when the number of vertices in said graph increase.
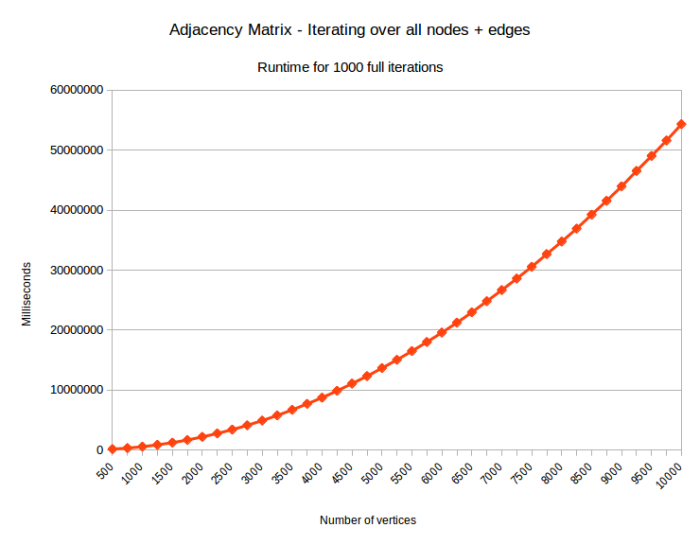
As shown above, there is indeed a quadratic relation between the number of vertices in an Adjacency Matrix and the total runtime when finding and iterating over all edges.
These measurements are the result of the code located at https://github.com/daankolthof/boost_graph_algorithms and were performed on an AWS EC2 t2.medium instance.
Algorithms
In this section, I will showcase the use of a few common graph algorithms, which are already built into the Boost Graph Library. Notice that, for breadth-first search, depth-first search and A* search, we make use of the visitor pattern, in which a visitor gets called whenever we visit a node or edge in the graph.
Breadth-first search
#include <array>
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/breadth_first_search.hpp>
#include "../../include/edge_tuple.hpp"
class bfs_visitor_impl : public boost::default_bfs_visitor {
public:
template < class Vertex, class Graph >
void examine_vertex(Vertex u, Graph& g)
{
std::cout << "Visited node: " << u << std::endl;
}
};
void bfs() {
const std::size_t vertex_count = 7;
const std::size_t edge_count = 6;
/*
Graph structure
0
/ \
/ \
1 2
/ \ / \
3 4 5 6
*/
const std::array<edge_tuple, edge_count> edges = { { {0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6} } };
using undirected_unweighted_graph = boost::adjacency_list<boost::listS, boost::vecS, boost::directedS>;
undirected_unweighted_graph g(edges.cbegin(), edges.cend(), vertex_count);
bfs_visitor_impl vis;
// A correct order would be: {0, 1, 2, 3, 4, 5, 6}
boost::breadth_first_search(g, 0u, boost::visitor(vis));
}
int main() {
bfs();
}
Depth-first search
#include <array>
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/depth_first_search.hpp>
#include "../../include/edge_tuple.hpp"
class dfs_visitor_impl : public boost::default_dfs_visitor {
public:
template < class Vertex, class Graph >
void discover_vertex(Vertex u, Graph& g)
{
std::cout << "Visited node: " << u << std::endl;
}
};
void dfs() {
const std::size_t vertex_count = 7;
const std::size_t edge_count = 6;
/*
Graph structure
0
/ \
/ \
1 2
/ \ / \
3 4 5 6
*/
const std::array<edge_tuple, edge_count> edges = { { {0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6} } };
using undirected_unweighted_graph = boost::adjacency_list<boost::listS, boost::vecS, boost::directedS>;
undirected_unweighted_graph g(edges.cbegin(), edges.cend(), vertex_count);
dfs_visitor_impl vis;
// A correct order would be: {0, 1, 3, 4, 2, 5, 6}
boost::depth_first_search(g, boost::visitor(vis).root_vertex(0u));
}
int main() {
dfs();
}
A*
#include <array>
#include <iostream>
#include <vector>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/astar_search.hpp>
#include "../../include/edge_tuple.hpp"
class astar_visitor_impl : public boost::default_astar_visitor {
public:
template < class Vertex, class Graph >
void examine_vertex(Vertex u, Graph& g)
{
std::cout << "Visited node: " << u << std::endl;
}
};
template < class Graph, class CostType >
class astar_heuristic_impl : public boost::astar_heuristic<Graph, CostType> {
public:
typedef typename boost::graph_traits< Graph >::vertex_descriptor Vertex;
CostType operator()(Vertex u) const {
// For simplicity, our goal state will always be 6, the closer the current vertex descriptor is to 6, the better.
return abs(6 - u);
}
};
void a_star() {
const std::size_t vertex_count = 7;
const std::size_t edge_count = 6;
/*
Graph structure
0
/ \
/ \
1 2
/ \ / \
3 4 5 6
*/
const std::array<edge_tuple, edge_count> edges = { { {0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6} } };
const std::array<std::size_t, edge_count> edge_weights = { 1, 1, 1, 1, 1, 1 };
using undirected_unweighted_graph = boost::adjacency_list<
boost::listS,
boost::vecS,
boost::directedS,
boost::no_property,
boost::property<
boost::edge_weight_t,
std::size_t>>;
undirected_unweighted_graph g(edges.cbegin(), edges.cend(), edge_weights.cbegin(), vertex_count);
astar_visitor_impl vis;
astar_heuristic_impl<undirected_unweighted_graph, std::size_t> heur;
// Expected order: {0, 2, 6, 5, 1, 4, 3}
boost::astar_search(
g,
0u,
heur,
boost::visitor(vis)
);
}
int main() {
a_star();
}
Topological Sort
#include <array>
#include <iostream>
#include <vector>
#include <boost/graph/adjacency_list.hpp>
#include <boost/graph/topological_sort.hpp>
#include "../../include/edge_tuple.hpp"
void topological_sort() {
const std::size_t vertex_count = 7;
const std::size_t edge_count = 6;
/*
Graph structure
0
/ \
/ \
1 2
/ \ / \
3 4 5 6
*/
const std::array<edge_tuple, edge_count> edges = { { {0, 1}, {0, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6} } };
using undirected_unweighted_graph = boost::adjacency_list<boost::listS, boost::vecS, boost::directedS>;
using vertex_descriptor = boost::graph_traits<undirected_unweighted_graph>::vertex_descriptor;
undirected_unweighted_graph g(edges.cbegin(), edges.cend(), vertex_count);
std::array<vertex_descriptor, vertex_count> result_order;
// A correct order would be: {3, 4, 1, 5, 6, 2, 0}
boost::topological_sort(g, result_order.begin());
for (const vertex_descriptor& v : result_order) {
std::cout << v << " ";
}
std::cout << std::endl;
}
int main() {
topological_sort();
}
Conclusion
The Boost Graph Library is a powerful library that simplifies the way graph data structures and algorithms can be used in C++. I highly recommend using it for any graph-related programming.
The measurement code, as well as the Boost Graph library examples, can be found at: https://github.com/daankolthof/boost_graph_algorithms.