Many applications within distributed networks require some sort of coordinator and/or leader to work. An example of this would a distributed database, where a coordinator controls which nodes within the network contain what data.
One problem arises with these leader-dependent algorithms: having a distributed system and/or algorithm depend on a leader introduces a single point of the failure in the entire network. If the leader is down, the rest of the system will either go down or as well, or be faulty in other ways (give unpredictable results, have out-of-date data, etc.).
To solve this problem and make distributed systems more stable and reliable, nodes can take over the leader role when the current leader of the system fails. Determining which node takes over in case of a leader failure is done through a so-called leader election algorithm.
In this post, I will give a brief overview of distributed networks and how they can be laid out/designed. Afterwards, I will discuss the Bully algorithm for leader election, including an example of this algorithm in action. The code for this algorithm can be found at: https://github.com/daankolthof/leader-election.
Distributed networks
Different topologies (designs) of distributed networks have different leader election algorithms that work best on them. This post focuses on fully connected networks, as these types of networks resemble the internet the most, with any machine being able to connect to any other machine. Some other well-known and well-researched topologies include bus networks, star networks and ring topologies, which have different leader election algorithms that work best.
Leader election in fully connected networks
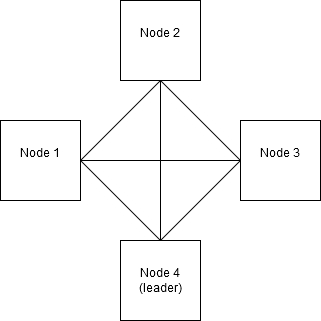
One of the leader election algorithms that works well on fully connected networks is the Bully algorithm. In this algorithm, every node within the network has an ID and a list of all other nodes in the network. Nodes can detect other nodes failing, and can initiate an election of a new leader if necessary.
The algorithm itself works as follows: If a node detects leader failure, it will send an election message to all nodes with a higher ID and will wait for a response to these messages.
If there’s no response after a certain amount of time, the node will promote itself to leader. If there is a response, it means there are nodes with higher IDs up and running, resulting in the current node to wait until one of the nodes with a higher ID elects itself as leader.
If the node detecting leader failure is the node with the highest ID, it will not send any election messages and immediately promote itself to new leader of the network.
Nodes receiving an election message will send back an alive message and will also start the leader election process themselves, sending out election messages to nodes with higher ID’s.
Once a node promotes itself to the new leader of the network, it will notify all other nodes of this, finishing the leader election process.
Leader election in action
An example of the Bully algorithm in action is given now. In this example, there are four nodes, of which the leader crashes/fails to respond.

Node 2 discovers this, and starts the leader election process, sending an election message to all higher nodes. In this case, the election message is sent only to node 3, as node 4 is down/unreachable.
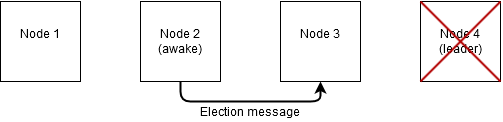
Node 3 receives the election message and responds with an alive message, indicating it is still up and running. Node 2 now knows there are nodes with higher IDs that are still up and running, and thus node 2 will wait for another node (with a higher ID) to complete the leader election process.
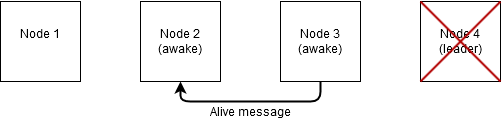
Node 3 will also start the leader election process itself. Since node 3 is the node with the highest ID of all the nodes that are still running, it elects itself as the new leader of the distributed system. It will inform the other nodes in the network of the fact that node 3 has elected itself as new leader.
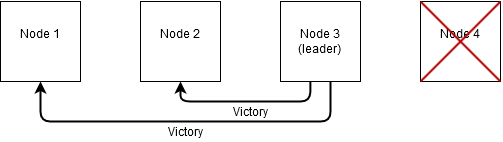
All other nodes that are still up and running now see node 3 as their new leader.
Runtime and efficiency
| Runtime | O(1) (constant time) |
| Number of messages sent | O(n^2) |
The runtime of the Bully algorithm is not dependent on the total number of nodes within the distributed network. This is because any node detecting a failure will immediately notify all nodes with higher IDs. This will end the leader election process immediately in case the node with the highest ID is up and running. If not, there is only one more step of message sending, as all nodes with higher IDs know leader election is in process, and will check once more if nodes with even higher IDs are up or not. This makes it so only two rounds of message sending are being done.
Despite the efficient runtime, the network usage of the algorithm is less efficient. An expected n^2 number of messages (with n the number of nodes within a network) will be sent. This runtime accounts for the worst-case scenario: the scenario in which every node notifies all other nodes with higher IDs.
Conclusion
The Bully algorithm for leader election is a good way to ensure that leader-dependent distributed algorithms work well. The algorithm provides quick recovery in case leader nodes stop working, although the network usage is not very efficient.
The source code for the Bully algorithm discussed in this post is available at: https://github.com/daankolthof/leader-election.